실전프로젝트 2일차 - 데이터 EDA 및 가설검정

카테고리 없음

실전프로젝트 2일차 - 데이터 EDA 및 가설검정

iron-min 2025. 12. 3. 20:51

1. 시각화 분석 및 EDA

시퀀스별로 전류 패턴이 있는걸 확인할 수 있습니다. 정상과 불량의 패턴이 다른지는 검증해봐야할것 같습니다.

시퀀스별로 전압 또한 패턴이 보여지는 모습입니다.

기초통계(불량, 양품으로만 나눠서 진행)

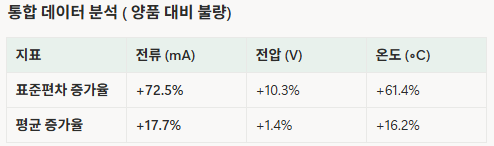
핵심 불량 패턴은 전류의 극심한 불안정성과 온도의 상승으로 집중. 전압 데이터는 이 두 가지 현상의 결과 또는 반응으로 해석
제 1원인: 전류의 통제불능

▶️ 분석: 표준편차 증가율에서 전류가 압도적인 1위(+72.5%)를 차지한다는 것은, 불량품 공정이 전류 제어에 가장 큰 문제를 겪었음을 의미. 불안정한 전류는 피막 파괴, 스파크 등을 유발하여 아노다이징 불량의 가장 직접적인 원인

제 2원인: 온도의 상승 및 불안정

▶️ 분석:

온도 표쥰편차(+61.4% 증가): 온도 변동성이 매우 높음
온도 평균/중위값 상승 (+16.2% / +33.3%): 공정 자체가 고온 조건에서 진행되었음을 확인시켜 줌
인과관계: 1차적으로 높은 전류(I)와 불안정한 저항(R)으로 인해 열이 발생했고, 이 열이 전해액의 온도를 상승 및 불안정하게 만들어 피막 용해 속도를 증가시켜 품질 저하를 초래
제 1,2원인으로 인한 전압의 상태 반영

▶️ 분석:

전압의 표준 편차 (+10.3% 증가): 전압의 변동성도 증가했지만, 전류의 변동성(+72.5%)와 비교하면 상대적으로 낮은 수준
경과: 아노 다지징 공정은 보통 정전류 모드로 작동함. 전류를 목표치에 맞추기 위해 전압(V)은 저항(R)의 변화에 따라 자동으로 변함(V=IR). 전류가 불안정하거나 피막 저항이 급변할 때, 공정은 전류를 유지하기 위해 전압을 더 높게, 더 자주 변경해야 했었고, 이것이 전압의 중위값 및 표준편차의 상승으로 나타남

라는 가설을 세웠습니다.

2. 가설검정

시각화에서 세워본 가설을 Mann-Whitney U 검정을 실시해 보았습니다.

2-1. 정규성검정

양품/불량품 데이터 정규성 검정

from scipy.stats import shapiro

# 실패 / 성공 데이터 분리
df_fail = df_mil[df_mil['failure'] == -1]
df_success = df_mil[df_mil['failure'] == 1]

# 시퀀스별 평균
df_success_avg = df_success.groupby('sequence_index').mean()
df_fail_avg = df_fail.groupby('sequence_index').mean()

# 정규성 검정할 컬럼 리스트
test_columns = ['volt','ampere','temperature','시간변화량(초)','두께변화량']

results = []

for col in test_columns:
    fail_stat, fail_p = shapiro(df_fail_avg[col])
    success_stat, success_p = shapiro(df_success_avg[col])

    results.append({
        'Column': col,
        'Fail_statistic': f'{fail_stat:.4f}',
        'Fail_p-value': f'{fail_p:.4f}',
        'Success_statistic': f'{success_stat:.4f}',
        'Success_p-value': f'{success_p:.4f}'
    })

result_df = pd.DataFrame(results)
print(result_df)

# 정규성 만족 컬럼 volt,ampere
# 정규성 만족 X 컬럼 temperature, 시간변화량, 두께변화량(success 데이터는 만족함)

장비별 데이터 정규성 검정

# rec1 / rec2 데이터 분리
df_rec1 = df_mil[df_mil['rec_num'] == 1]
df_rec2 = df_mil[df_mil['rec_num'] == 2]

# 시퀀스별 평균
df_rec1_avg = df_rec1.groupby('sequence_index').mean(numeric_only=True)
df_rec2_avg = df_rec2.groupby('sequence_index').mean(numeric_only=True)

# 정규성 검정할 컬럼 리스트
test_columns_rec = ['volt','ampere','temperature','시간변화량(초)','두께변화량']

results = []

for col in test_columns_rec:
    rec1_stat, rec1_p = shapiro(df_rec1_avg[col].dropna())
    rec2_stat, rec2_p = shapiro(df_rec2_avg[col].dropna())

    results.append({
        'Column': col,
        'Rec1_statistic': f'{rec1_stat:.4f}',
        'Rec1_p-value': f'{rec1_p:.4f}',
        'Rec2_statistic': f'{rec2_stat:.4f}',
        'Rec2_p-value': f'{rec2_p:.4f}'
    })

result_df_rec = pd.DataFrame(results)
print(result_df_rec)

# 정규성 만족 컬럼 volt, 두께변화량
# 정규성 만족 X 컬럼 ampere,temperature,시간변화량(초)

일부 정규성이 만족하지 않는 컬럼들이 많아서 Mann-Whitney U 검정을 하기로 했습니다.

2-2. 양품/불량품간 비교

시각화

# subplot 설정
fig, axes = plt.subplots(nrows=1, ncols=len(test_columns), figsize=(4*len(test_columns), 5))

for i, col in enumerate(test_columns):
    sns.violinplot(data=df_mil, x='failure', y=col, ax=axes[i], inner='quartile',palette='Set2')
    axes[i].set_title(col)
    axes[i].set_xlabel('')
    axes[i].set_ylabel('')

plt.tight_layout()
plt.show()

검정

from scipy.stats import mannwhitneyu

mw_results_failure = []

for col in ['volt', 'ampere', 'temperature', '시간변화량(초)', '두께변화량']:
    stat, p = mannwhitneyu(df_fail_avg[col],
                           df_success_avg[col],
                           alternative='two-sided')

    mw_results_failure.append({
        'Column': col,
        'U-statistic': round(stat, 4),
        'p-value': round(p, 4),
        '유의성 (p < 0.05)': '차이가 있다' if p < 0.05 else '차이가 없다'
    })

mw_df_failure = pd.DataFrame(mw_results_failure)
print(mw_df_failure)

2-2. 장비별 특성치 비교

시각화

# subplot 설정

test_columns_rec = ['volt','ampere','temperature','시간변화량(초)','두께변화량']
fig, axes = plt.subplots(nrows=1, ncols=len(test_columns_rec), figsize=(4*len(test_columns_rec), 5))

for i, col in enumerate(test_columns_rec):
    sns.violinplot(data=df_mil, x='rec_num', y=col, ax=axes[i], inner='quartile',palette='Set2')
    axes[i].set_title(col)
    axes[i].set_xlabel('')
    axes[i].set_ylabel('')

plt.tight_layout()
plt.show()

검정

mw_results_rec = []

for col in ['volt', 'ampere', 'temperature', '시간변화량(초)', '두께변화량']:
    stat, p = mannwhitneyu(df_rec1_avg[col],
                           df_rec2_avg[col],
                           alternative='two-sided')

    mw_results_rec.append({
        'Column': col,
        'U-statistic': round(stat, 4),
        'p-value': round(p, 4),
        '유의성 (p < 0.05)': '차이가 있다' if p < 0.05 else '차이가 없다'
    })

mw_df_rec = pd.DataFrame(mw_results_rec)
print(mw_df_rec)

2-3. 양품/불량품 간 산포차이 유의성 검정

import numpy as np

cols = ['volt', 'ampere', 'temperature', '시간변화량(초)', '두께변화량']

mw_var_results = []

for col in cols:
    # 시퀀스별 분산 계산
    fail_var = df_fail.groupby('sequence_index')[col].var()
    success_var = df_success.groupby('sequence_index')[col].var()

    # Mann-Whitney U test (양측 검정)
    stat, p = mannwhitneyu(
        fail_var,
        success_var,
        alternative='two-sided'
    )

    mw_var_results.append({
        'Column': col,
        'U-statistic': round(stat, 4),
        'p-value': round(p, 4),
        '유의성 (p < 0.05)': '차이가 있다' if p < 0.05 else '차이가 없다'
    })

mw_var_df = pd.DataFrame(mw_var_results)
print(mw_var_df)

2-4. 양품/불량품 간 특성치 변화율 최대치 비교 검정

순간변화율 계산

# 1) 정렬
df_mil = df_mil.sort_values(['sequence_index', 'pk_datetime'])

# 2) ampere에 대한 dI/dt
df_mil['dI_ampere'] = df_mil.groupby('sequence_index')['ampere'].diff()
df_mil['dt_ampere'] = df_mil.groupby('sequence_index')['pk_datetime'].diff().dt.total_seconds()
df_mil['dI_dt_ampere'] = df_mil['dI_ampere'] / df_mil['dt_ampere']

# 3) volt에 대한 dV/dt
df_mil['d_volt'] = df_mil.groupby('sequence_index')['volt'].diff()
df_mil['dt_volt'] = df_mil.groupby('sequence_index')['pk_datetime'].diff().dt.total_seconds()
df_mil['dV_dt_volt'] = df_mil['d_volt'] / df_mil['dt_volt']

# 4) temperature에 대한 dT/dt
df_mil['d_temperature'] = df_mil.groupby('sequence_index')['temperature'].diff()
df_mil['dt_temperature'] = df_mil.groupby('sequence_index')['pk_datetime'].diff().dt.total_seconds()
df_mil['dT_dt_temperature'] = df_mil['d_temperature'] / df_mil['dt_temperature']

# 5) 두께변화량에 대한 d(thickness)/dt
df_mil['d_thickness'] = df_mil.groupby('sequence_index')['두께변화량'].diff()
df_mil['dt_thickness'] = df_mil.groupby('sequence_index')['pk_datetime'].diff().dt.total_seconds()
df_mil['dThickness_dt'] = df_mil['d_thickness'] / df_mil['dt_thickness']

# 6) 시퀀스별 최대 절대 변화율 계산 (ampere + volt + temperature + 두께변화량)
max_change_rate = (
    df_mil.groupby('sequence_index')
          .agg(
              max_abs_dI_dt_ampere   = ('dI_dt_ampere',    lambda x: np.nanmax(np.abs(x))),
              max_abs_dV_dt_volt     = ('dV_dt_volt',      lambda x: np.nanmax(np.abs(x))),
              max_abs_dT_dt_temp     = ('dT_dt_temperature', lambda x: np.nanmax(np.abs(x))),
              max_abs_dThickness_dt  = ('dThickness_dt',   lambda x: np.nanmax(np.abs(x)))
          )
          .reset_index()
)

max_fail_rate = max_change_rate.merge(df_fail_avg, on='sequence_index',how='left').dropna()
max_success_rate = max_change_rate.merge(df_success_avg, on='sequence_index',how='left').dropna()

순간변화율 검정

mw_results_rate = []

for col in ['max_abs_dV_dt_volt', 'max_abs_dI_dt_ampere', 'max_abs_dT_dt_temp', 'max_abs_dThickness_dt']:
    stat, p = mannwhitneyu(max_success_rate[col],
                           max_fail_rate[col],
                           alternative='two-sided')

    mw_results_rate.append({
        'Column': col,
        'U-statistic': round(stat, 4),
        'p-value': round(p, 4),
        '유의성 (p < 0.05)': '차이가 있다' if p < 0.05 else '차이가 없다'
    })

mw_results_rate = pd.DataFrame(mw_results_rate)
print(mw_results_rate)

3. 정리

시각화를 했을때는 양품과 불량품간의 차이가 있을줄 알았는데 검정을 해보니 차이가 나지 않는다는것을 알았습니다.

데이터를 따로 계산해봐도 차이가 큰데 검정이 잘못될수도 있고 정말 유의하지 않을 수도 있을 것 같습니다.

추측하건데 아마 시계열 분석까지는 진행해야 불량품을 선별할 수 있지 않을까 생각합니다.